導入
従来の学習法は暗記やワークシートに大きく依存しているため、多くの子どもたちが算数で苦労しています。数字とその関係性を理解できないと、生徒たちは挫折感を抱き、算数から孤立してしまうことがよくあります。そこで、モンテッソーリ算数教材が大きな力を発揮します。モンテッソーリ算数は、子どもたちに抽象的な概念を暗記させるのではなく、実践的な学習を通して数字を学びます。子どもたちは、数字を目で見て、触って、そして操作することで、自分にとって理解しやすい方法で算数を理解できるようになります。
紙に書かれた数字を見るだけで足し算を学ぼうとする子どもを想像してみてください。そして、金色のビーズや数字棒といったモンテッソーリ算数教材を使って、物理的に量を足し算したり分けたりしている子どもと比べてみてください。後者の子どもの方が概念をより早く理解し、その過程を楽しんでいます。多くの子どもは、このような方法に取り組まなくても算数不安を抱き、学習の進歩がさらに難しくなります。モンテッソーリ算数は、算数を幼児教育の自然で楽しい一部にすることで、こうした困難を解消します。
モンテッソーリ数学メソッドを使って、子どもたちは幼いころから強い数学的思考力を養います。 紙やすり、スピンドルボックス、百マスボードなどの道具を使って、子どもたちは論理的かつ体系的に数字を学びます。モンテッソーリ算数カリキュラムは、子どもたちが具体的な学習から抽象的な学習へと移行し、算数への自信を育むことを可能にします。この記事では、算数を最大限に活用する方法についてご紹介します。 モンテッソーリ教材これらがなぜ効果的かを説明し、数学の学習を楽しく有意義なものにする方法を示します。

モンテッソーリ数学とは何ですか?
モンテッソーリ数学は 実践的で子ども中心の数学学習アプローチモンテッソーリ算数教材を通して数字を学ぶことで、暗記に頼るのではなく、子どもたちが具体的かつ意味のある方法で算数を探求できるようにします。抽象的な思考に移る前に、子どもたちはサンドペーパー、数字棒、金色のビーズなどの道具を使って、数学の概念を実際に見て触れることができます。このメソッドは、子どもたちが幼い頃から数字、パターン、そして問題解決を理解するのに役立つ、力強い数学的思考力を育みます。
モンテッソーリ算数カリキュラムでは、子どもたちは数え方や数の認識といった簡単な活動から始め、その後、足し算、引き算、掛け算、割り算といった複雑な計算へと進んでいきます。その目的は、数を教え、論理的思考力と算数への深い理解を育むことです。
モンテッソーリ算数教育の基本原則
モンテッソーリ算数教育法は、体系的でありながら柔軟なアプローチで算数を指導します。主な原則は以下のとおりです。
- 具体的学習から抽象的学習へ – モンテッソーリでは、子どもたちはまず数学の道具を使って学習します書かれた数字や記号に移行する前に、金色のビーズや紡錘形の箱などの文字を使用します。
- 実践的な探検 – 子どもたちは講義を聞く代わりに、積極的に数学モンテッソーリ教材を操作して、数学的関係を自主的に発見します。.
- 自分のペースで学習 – それぞれの子供が自分のペースでモンテッソーリ数学カリキュラムを進め、先に進む前に概念を完全に理解できるようにします。
- 数学的思考力の発達 – マリア・モンテッソーリ博士は、適切な道具を与えれば、子どもたちは生まれながらに数学を理解する能力を持っていると信じていました。モンテッソーリの算数教育法は、算数を感覚体験にすることで、この自然な能力を育みます。
これらの原則に従うことで、モンテッソーリ数学は子供たちの自信と数字への愛を育み、将来の学習のための強固な基盤を築きます。
モンテッソーリ算数と伝統的な算数の違い
モンテッソーリ教育における算数の教え方は、従来の教育法とは大きく異なります。従来の教室では、子どもたちは公式や手順を暗記するだけで、完全に理解することはできません。一方、モンテッソーリ教育では、体験学習を重視し、子どもたちが実践的な活動を通して数学的な思考力を育むことを目指しています。
| 側面 | モンテッソーリ数学 | 伝統的な数学 |
|---|---|---|
| 学習アプローチ | 実践的な探究のために数学モンテッソーリ教材を使用する | 教科書やワークシートに頼る |
| コンセプト開発 | 具体的な理解から抽象的な理解へ | 早い段階で抽象的なシンボルに焦点を当てる |
| ペース | 子ども主導で、前に進む前に習熟できるようにする | 教師主導、固定されたカリキュラムのタイムライン |
| エラー訂正 | 繰り返しが多く、暗記中心だと感じることがある | 教師からの外部的な矯正に頼る |
| 婚約 | 数学をインタラクティブで楽しいものにします | 反復的で暗記中心だと感じる |
モンテッソーリ算数教材は、子どもたちが数字を暗記するのではなく、見て、触って、理解するために使われます。このアプローチは算数をより意味のあるものにし、挫折感を軽減し、 子どもたちは生涯にわたって役立つ問題解決能力を身につけます。


モンテッソーリ教育における数学の重要性
数学は単なる数字ではありません。それは思考方法です。モンテッソーリ算数では、算数は暗記すべき科目ではなく、子どもの発達の自然な一部として導入されます。モンテッソーリ算数教材を通して、子どもたちは数字やパターンを実際に体験し、問題解決能力、論理的推論能力、批判的思考力の強固な基盤を育みます。
モンテッソーリ算数が数学的思考力を育む仕組み
従来の教室では、子どもたちは方程式や公式の意味を真に理解することなく、暗記させられることがよくあります。これとは対照的に、モンテッソーリ算数は体験学習を重視し、子どもたちの探究心と発見を通して数学的な思考力を育みます。金色のビーズ、数字棒、スピンドルボックスなどの道具を使うことで、子どもたちは数字を視覚的に捉え、抽象的な概念を理解しやすくなります。子どもたちは、手を使って材料を扱うことで、数量、位取り、数学的な計算をより深く理解します。
モンテッソーリ算数が幼児期の認知発達に与える影響
研究によると、早期に実践的な算数活動に触れることで、認知発達が著しく向上することが示されています。モンテッソーリ算数メソッドは、それぞれの子どものペースに合わせて、体系的でありながら柔軟な学習体験を提供します。幼い学習者は、足し算、引き算、掛け算、割り算に進む前に、並べ替え、数え上げ、パターン認識を学習します。こうした早期の数との関わりは、子どもたちの集中力、記憶力、そして問題解決能力を育み、将来の学業成績向上に不可欠な能力となります。
モンテッソーリ算数が幼児教育に効果的な理由
子どもたちは、積極的に関わることで最もよく学びます。モンテッソーリ算数カリキュラムは、子どもたちがプレッシャーを感じることなく概念を探求できるよう、自分のペースで学習できるように設計されています。間違った答えを失敗と捉える従来の学習方法とは異なり、モンテッソーリ算数は、子どもたちが自ら間違いを正すことを促します。例えば、百マスボードの使い方を間違えたとしても、子どもたちは自ら間違いに気づき、修正することができます。このプロセスを通して自信と回復力が育まれ、算数は恐怖ではなく探求の対象となります。
モンテッソーリ算数教授法
モンテッソーリにおける算数の指導 モンテッソーリ教育は、独自の子ども中心のアプローチを採用しています。暗記から始めるのではなく、 子どもたちがまず数字に対する直感的な理解を育むことを目指します。これは、具体的な思考から抽象的な思考へと徐々に移行していく、体系的な学習体験を通して行われます。
モンテッソーリ算数指導の基本原則
- 実践的な探検 – 学習は教科書ではなく、数学モンテッソーリ教材を通じて行われます。
- 段階的な進歩 – 概念が互いに積み重なり、論理的な学習シーケンスが保証されます。
- 自主学習 – 子どもたちは不必要なプレッシャーを受けることなく、自主的に数学を探求します。
- 材料によるエラー訂正 – モンテッソーリ数学教材の多くは自己修正型であり、子供たちは間違いから学ぶことができます。
モンテッソーリ算数の4Cフレームワーク
モンテッソーリ算数カリキュラムは、数字を教えるだけでなく、生活に不可欠なスキルを育みます。モンテッソーリ算数の最も価値ある側面の一つは、4Cフレームワークを重視していることです。
1. 批判的思考
モンテッソーリ算数では、子どもたちに直接的な答えを与えることはありません。モンテッソーリ算数教材を用いて概念を探求し、観察、試行錯誤、そして自己修正を通して学びます。例えば、足し算と引き算の練習では、子どもたちは単に方程式を暗記するのではなく、実際に物を動かして数字の変化を観察します。この実践的なアプローチは、子どもたちが問題解決能力と数学的パターンを自主的に分析する能力を育むのに役立ちます。
2. コラボレーション
従来の教室とは異なり算数は個人課題であることが多いですが、モンテッソーリ算数アクティビティは仲間同士の学習を促します。子どもたちはモンテッソーリメソッドを用いて協力して学習します。 数学を学び、発見したことを話し合い、互いに助け合いながら解決策を見つけます。多年齢クラスでは、低学年の生徒は高学年の生徒を観察し、高度な概念への理解を深め、高学年の生徒は他の生徒に教えることで知識を強化します。この協働的な環境は、自信、チームワーク、そして数学の原理へのより深い理解を育みます。
3. 創造性
モンテッソーリ教育における算数は、公式を暗記することではなく、数字同士の関係性を発見することです。モンテッソーリ算数カリキュラムでは、子どもたちが問題に多様なアプローチで取り組むことを可能にします。百マス盤のパターンを探ったり、数を割る様々な方法を試したりすることで、子どもたちは単純な計算を超えた創造的な問題解決能力を育みます。この柔軟性により、子どもたちは算数を、厳格なルールの羅列ではなく、ダイナミックで魅力的な科目として捉えることができるようになります。
4. コミュニケーション
モンテッソーリ算数では、子どもたちは自分の思考過程を言葉と視覚で表現することが奨励されます。モンテッソーリ算数で算数用具を使う際、子どもたちは自分の推論を先生やクラスメイトに説明することがよくあります。算数の概念を言葉で表現することは、子どもたちの理解を深め、複雑な考えを明確に表現する能力を高めるのに役立ちます。このスキルは、時間の経過とともに、より優れた推論力、体系的な思考、そして数学的な議論における自信へとつながっていきます。
モンテッソーリ数学は、4C フレームワークを統合することにより、子供たちが数学的能力と生涯学習に不可欠なスキルを身に付けられるようにします。
モンテッソーリは具体的な概念から抽象的な概念まで算数をどう教えるのか
モンテッソーリ算数の大きな特徴の一つは、具体的な学習から抽象的な学習へと段階的に進めることです。モンテッソーリ算数教育法では、数字や記号を最初に導入するのではなく、子どもたちが数字や方程式の書き方を学ぶ前に、数学の概念を深く実践的に理解できるようにしています。
子どもたちは具体的な段階で数量、位取り、数学的演算を探求します 実践的な経験を通して、子どもたちは数字を実際に見て操作し、数の関係性に関する確固たる基礎を築くことができます。繰り返し練習することで、パターンを認識し、足し算、引き算、掛け算、割り算の直感的な感覚を養います。
子どもたちが具体的なレベルで自信と理解を示すようになると、徐々に抽象的な思考へと移行していきます。数字と記号を関連付け、紙の上で問題を解き、暗算の戦略を駆使して計算するようになります。この段階に達すると、算数はもはや単なる暗記ではなく、子どもたちにとって意味のある論理体系へと変化していきます。
モンテッソーリ数学カリキュラムのこの構造化されたアプローチにより、子供たちは数学を単に学ぶだけでなく、真に理解できるようになります。

モンテッソーリ数学カリキュラムの構造
モンテッソーリ算数カリキュラムは、子どもたちが段階的に数学的理解を深められるよう、綿密に構成された順序に従っています。抽象的な概念にいきなり飛びつくのではなく、足し算、引き算、掛け算、割り算といった正式な計算を学ぶ前に、子どもたちが量の感覚、位取り、数の関係性をしっかりと身につけられるよう配慮されています。
この構造化された進行により、子供たちは数学の事実を単に暗記するだけでなく、数字の仕組みを真に理解できるようになり、数学的推論を実際の状況に適用しやすくなります。
1. モンテッソーリ算数の触覚体験
モンテッソーリ算数の最初のステップは、数字との物理的なつながりを築くことです。子どもたちが「5」や「10」といった記号を理解する前に、数字を実際に体験する必要があります。触覚、動き、観察といった感覚を駆使して、実生活における数量を探究していきます。
例えば、子どもたちは物を分類したり、グループ分けしたり、大きさ、重さ、長さの違いを認識したりすることに時間を費やすかもしれません。こうした初期の活動は、数字の関係性を具体的に理解するのに役立ち、後に抽象的な数学を理解するのがはるかに容易になります。
この段階では、算数は記号や方程式ではなく、現実世界での数字の意味について学びます。物理的な体験を通して数字に触れることで、子どもたちは算数を暗記させられる単調な科目として捉えるのではなく、自然な好奇心を育みます。
2. 数量と数:数の感覚を養う
子どもたちが現実世界の量を認識できるようになると、数字と記号の関係性を学びます。この段階で、子どもたちは数字記号(1、2、3など)を実際の量と関連付けます。
しかし、モンテッソーリ数学では、単に数字の名前を暗記するのではなく、子供たちは体系的に数字を学習し、それぞれの数字がその前後の数字とどのように関連しているかを理解します。
- 機械的な繰り返しではなく、実際の物を使って前方と後方に数えることを学びます。
- 実践的な練習を通して奇数と偶数を認識します。
- 簡単なパターンとシーケンスを理解し始めます。これは後で掛け算と割り算に役立ちます。
子どもたちは、数字を暗唱するだけでなく、実際に数字に触れることで、数字の関係性に対する深い感覚を養います。自信を持って柔軟に数学に取り組むことができるようになります。
3. 十進法の紹介
小数点を理解することは、モンテッソーリ算数における重要な転換点です。「10個で10になる」「10個で100になる」とただ教えられるのではなく、子どもたちはこれらの関係性を実際に体験します。
- 1、10、100、1000 のグループを物理的に操作して、数字のスケールを理解します。
- 位取りの基礎となる、数字を 10 個ずつグループ化する方法を学びます。
- 数字は単なる個別の単位ではなく、予測可能なルールに従う構造化されたシステムの一部であることを学びます。
子どもたちがより高度な算数に達する頃には、位取りについてしっかりと理解しており、複雑な計算もずっと簡単に理解できるようになります。
4. 数学的演算:加算、減算、乗算、除算
数の関係と小数点以下を習得した後、子どもたちは算数の計算へと進みます。しかし、暗記に頼る従来の算数教育とは異なり、モンテッソーリ算数は、実践的で本格的な探究を通して計算を学びます。
- 追加子どもたちは「2 + 3 = 5」と暗記する代わりに、実際に2つの量を足し合わせて、その結果を自分で確認します。これにより、足し算はグループを合わせることであるという概念が強化されます。
- 減算子どもたちは、ある量をグループから実際に取り除き、残った量を正確に確認します。これは、引き算が2つの量の差を求めることだと理解するのに役立ちます。
- 乗算: 子供たちは掛け算を九九を暗記する代わりに繰り返しの足し算として学ぶ数字間のパターンや関係性を認識し、掛け算をより直感的に理解できるようになります。
- 分割: 割り算は均等にグループ化するものとして導入され、割り算とは量を小さなグループに公平に分割することであると子供たちに理解させます。
この段階で、子どもたちは答えを計算する方法を学び、それぞれの演算についての概念的な理解を深めます。
モンテッソーリ算数カリキュラムは、暗記の前に理解を深めることを目的として設計されており、子どもたちが単に公式を覚えるのではなく、数学の概念を真に理解できるようにします。カリキュラムの各段階は、次の段階への準備を整え、論理的で自然な学習の進行を生み出します。
子どもたちは、複雑な問題を解決できるようになると、数字に怖気づくことがなくなります。何年もかけて数学を有意義に探求し、経験してきたため、安心感と自信を持てるようになります。


必須数学モンテッソーリ教材
モンテッソーリ算数教材はモンテッソーリ算数メソッドの基礎であり、子どもたちが実践的な探究を通して強い数学的思考力を育むのに役立ちます。暗記に頼る従来の教育方法とは異なり、モンテッソーリ算数教材は子どもたちが 数字と物理的にやりとりする抽象的な概念を明確かつ直感的に理解できるようになります。
算数モンテッソーリ教材を使うことで、子どもたちは数学の概念を目で見て、触って、そして操作することで、問題解決能力、論理的思考力、そして数への深い理解を育みます。すべての教材は段階的な学習をサポートし、子どもたちが自分のペースで具体的な経験から抽象的な思考へと進んでいくことを可能にします。
算数モンテッソーリ教材の主な特徴
すべてのモンテッソーリ教材は、モンテッソーリ算数の指導に実践的な特定の原則に従っています。これらの教材は単なる学習補助教材ではなく、子どもたちが自発的に数、計算、そして数学的関係を探求することを可能にします。
- 実践的な学習アプローチ:
モンテッソーリ算数教材は、子どもたちに触覚体験を提供し、数字を紙の上で見るだけでなく、実際に手で触れる機会を与えます。このアプローチは、従来の学習方法では得られない、数感覚と問題解決能力を強化します。
- 自己修正と自立学習:
算数モンテッソーリ教材の各ピースには、エラーコントロール機能が組み込まれており、子どもたちが自主的に間違いを認識し、修正することができます。この機能は、子どもたちが単に間違いを指摘されるのではなく、自ら探求することで間違いを発見するため、自信と批判的思考力を育みます。
- 具体的から抽象的への進歩:
モンテッソーリ算数教材は、論理的な学習順序に沿って構成されています。子どもたちは、実際の量を表す物理的な物体から始め、記号や方程式へと進みます。この段階的な移行により、より複雑なトピックに進む前に、各概念を完全に理解することができます。
- 多感覚エンゲージメント:
モンテッソーリ算数教材は、視覚、触覚、運動といった複数の感覚を刺激し、子どもたちが数字と強い精神的なつながりを築くのに役立ちます。この多感覚学習体験は、概念をより長く記憶にとどめ、より深く理解することを可能にします。
- 実世界のアプリケーション:
モンテッソーリ算数教材は、子どもたちが算数の計算を学ぶだけでなく、その実践的な応用も理解できるよう構成されています。子どもたちは、日常生活における数字の働きを理解するのに役立つアクティビティに参加することで、モンテッソーリ算数が教室の枠を超えた学びの場としての重要性を実感します。
年齢に応じたモンテッソーリ算数教材
モンテッソーリ数学カリキュラムは、発達段階に応じてモンテッソーリ数学教材を導入し、子供たちが自分の認知能力に合った方法で数学を学習できるように設計されています。
- 幼児期(3~6歳):基礎算数モンテッソーリ教材の紹介:
この段階から、子どもたちはモンテッソーリ算数教材を使い始め、数の認識、量、基本的な計算を学びます。教材は物理的な探究に重点を置き、子どもたちが記号を扱う前に、現実世界の文脈で数を理解するのを促します。 - 触覚体験を通じて数値関係を理解する。
- 数え方、分類方法、パターンの認識方法を学びます。
- 実践的なアクティビティを通じて、足し算と引き算の直感的な感覚を養います。
- 小学校低学年(6~9歳):算数モンテッソーリ教材で理解を深める:
子どもたちは成長するにつれて、モンテッソーリ算数教材へと移行し、位取り、より重要な数、より複雑な計算を学びます。この段階では、問題解決能力と推論能力に重点が置かれ、子どもたちが数学の概念を様々な状況に応用できるよう支援します。 - 10 進法と位取りについて調べます。
- 段階的な学習活動を通じて掛け算と割り算を理解します。
- 構造化された実践的な演習を使用して数学の流暢性を強化します。
- 小学校高学年(9~12歳):数学モンテッソーリ教材を使った抽象的思考:
この段階では、子どもたちは基本的な計算の段階を超え、分数、小数、代数的思考を導入するモンテッソーリ算数教材を使い始めます。これらの教材は、子どもたちが抽象的な推論へと導き、数字だけで問題を解く前に、数学の原理を深く理解できるようにします。 - 分数と小数に関する強固な基礎を身につけます。
- 数学モンテッソーリ教材を使用して高度な問題解決スキルを適用します。
- 数学の概念と現実世界の応用とのつながりを探ります。
モンテッソーリ数学は、年齢に応じて体系的にモンテッソーリ数学教材を導入することで、子どもたちが発達のあらゆる段階で数字に対する深く永続的な理解を身に付けられるようにします。
コア数学モンテッソーリ教材とその機能
モンテッソーリ算数教材は、基本的な数の認識から複雑な問題解決まで、子どもたちを段階的に導くように設計されています。これらの教材はモンテッソーリ算数メソッドに基づいており、子どもたちが抽象的な推論に進む前に、数学的な概念を体験できるようにします。
完全で構造化された概要を提供するために、モンテッソーリ数学教材を年齢層と教育レベル別に分類し、モンテッソーリ数学カリキュラムで使用されるすべての教材が含まれ、説明されるようにします。
乳幼児(0~3歳) - 早期の感覚と空間認識
この段階では、子供たちは直接的な数字の作業ではなく、感覚の探究、空間認識、パターン認識を通じて初期の数学的思考を発達させます。
| 素材 | 関数 | 数学的概念の導入 |
|---|---|---|
| 物体の永続性ボックス | 問題解決と空間的推論を奨励する | 初期の論理と予測 |
| ノブ付きシリンダー | サイズの区別と順序付けに役立ちます | 測定と比較 |
| 積み重ねと入れ子のカップ | 高さ、大きさ、順序についての理解を深めます | 順序付けとパターン化 |
| 形状分類ボックス | 形状認識と分類を促進する | 初期の幾何学と分類 |
| ペグ上のリング | 一対一対応をサポート | 数え方の基礎 |
| 木製のカウントディスク | 数字とグループ分けへの早期の触れ合い | 数量認識 |

幼児期(3~6歳) - 数字と基本的な計算の入門
この段階で子供たちは基本的な数感覚を発達させます 実践的な体験を通して、数学の基礎概念を学びます。数量、数の認識、そして簡単な計算の強固な基礎を築くことが目標です。
| 素材 | 関数 | 数学的概念の導入 |
|---|---|---|
| ナンバーロッド | 数の順序付けと長さの比較を発達させる | 数え方と数値関係 |
| サンドペーパー番号 | 触覚的なトレースを通して数字の書き方を教える | 数字認識 |
| スピンドルボックス | 数え方を強化し、ゼロを導入する | 量の理解 |
| カードとカウンター | 子どもたちが数字と実際の量を関連付けるのを助ける | 一対一対応 |
| ティーン&テンボード(セギンボード) | 11~99の数字と位取りを紹介します | 初期の位取り |
| ゴールデンビーズ(イントロセット) | 10進法(一、十、百、千)を紹介します | 10進法 |
| ビーズ階段 | 数の順序と足し算を強化する | 初期の算術 |
| 百板 | 100までの数え方と数字認識をサポート | 番号順 |
| 追加ストリップボード | 足し算を視覚化して練習するのに役立ちます | 量の加算と結合 |
| 引き算ストリップボード | 物理モデルを用いた減算を導入する | 「取り除く」こととしての引き算 |
| ヘビゲーム | 数字の組み合わせと簡単な足し算を強化します | 初期の暗算 |
| 幾何学的なキャビネット | 幾何学的形状と特性を紹介する | 基本的な幾何学 |
| 建設的な三角形 | 形の形成と空間認識を促進します | 形状の構成と認識 |

小学校低学年(6~9歳) - 数の感覚と計算を広げる
子どもたちは進歩するにつれて、複雑な位取り、分数、多桁の演算を紹介する、より高度な数学モンテッソーリ教材に移行します。
| 素材 | 関数 | 数学的概念の導入 |
|---|---|---|
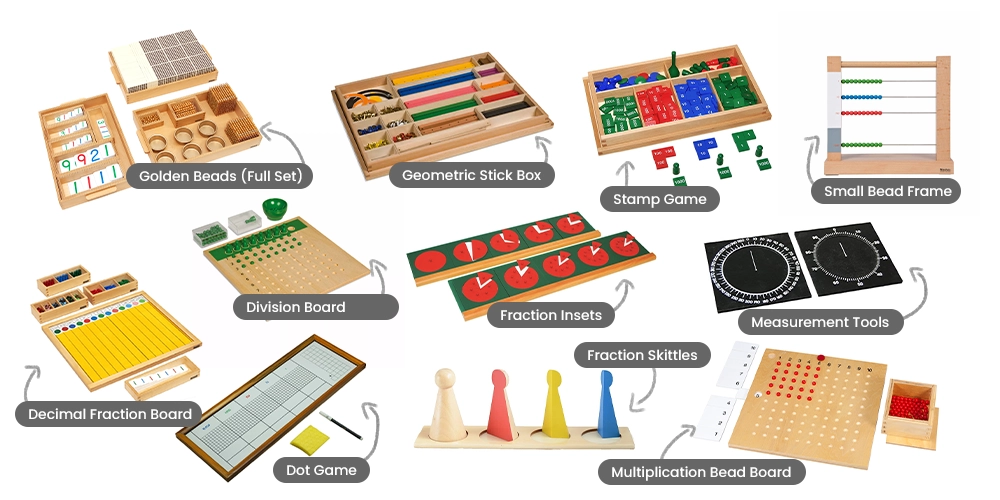
| ゴールデンビーズ(フルセット) | 位取りと算数の理解を深めます | 10進法と位取り |
| スタンプゲーム | コンクリート材料と筆算の橋渡し | 多桁の加算と減算 |
| ドットゲーム | 視覚的なグループ化を通じて位取りを強化する | 位取りと加算の概念 |
| 小さなビーズフレーム | 複数桁の加算と減算をサポート | 大きな数の算術 |
| かけ算ビーズボード | 子供が掛け算の計算を覚えるのに役立ちます | 繰り返し加算としての乗算 |
| 部門委員会 | 平等なグループ分けとして分割を強化する | 基本的な分割原則 |
| 分数インセット | 視覚的な表現で分数の概念を紹介します | 基本的な分数 |
| 分数スキットルズ | 子どもたちが分数を比較したり操作したりするのに役立ちます | 分数の関係 |
| 小数ボード | 分数を小数表記に結び付ける | 小数と分数の関係 |
| 幾何学的なスティックボックス | 角度、三角形、幾何学的構成を教える | 基本的な幾何学の原理 |
| 測定ツール(定規、分度器) | 測定と比較を導入する | 長さと角度の測定 |
上級小学校(9~12歳) - 算数、分数、代数の習得準備
この段階では、子供たちは実践的な数学モンテッソーリ教材からより抽象的な数学的推論へと移行し、代数、幾何学、問題解決の準備をします。
| 素材 | 関数 | 数学的概念の導入 |
|---|---|---|
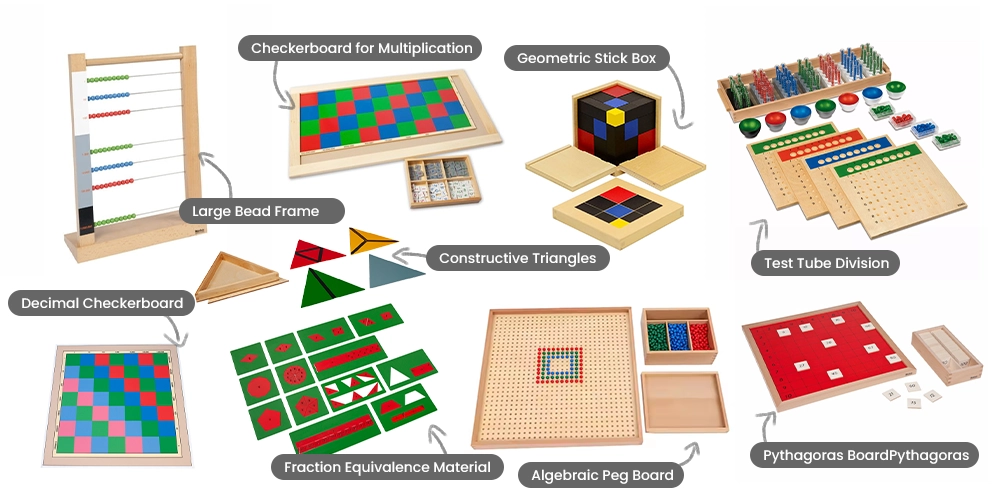
| 大きなビーズフレーム | 複数桁の乗算と除算をサポート | 多段階演算 |
| 掛け算のチェッカーボード | 複雑な掛け算を視覚化するのに役立ちます | 高度な掛け算 |
| 試験管部門 | 長い割り算を物理的なステップに分解します | 長除算の概念 |
| 小数点チェッカーボード | 小数の掛け算と演算を強化する | 高度な小数計算 |
| 分数等価材料 | 分数間の関係を示す | 同値分数 |
| 二項式キューブと三項式キューブ | 代数式を導入する | 代数の基礎概念 |
| 代数ペグボード | 高度な幾何学 | 代数的問題解決 |
| 建設的な三角形(上級セット) | 幾何学的な関係を探る | 高度な幾何学 |
| ピタゴラスボード | ピタゴラスの定理を実証する | ピタゴラスの定理 |
思春期(12~18歳) - 抽象代数、幾何学、そして現実世界の数学
モンテッソーリ中学校および高等学校では、生徒は現実世界の応用と実践的な数学モンテッソーリ教材を組み合わせて、抽象的な問題解決に移行します。
| 素材 | 関数 | 数学的概念の導入 |
|---|---|---|
| 代数タイル | 方程式の解法と多項式演算をサポート | 代数式 |
| 方程式ペグボード | 代数関係を視覚化するのに役立ちます | 線形方程式 |
| 幾何学的立体 | 3Dジオメトリの理解を強化 | 3D形状のプロパティ |
| 上級三角法ボード | 三角関数の紹介 | 正弦、余弦、正接 |
| グラフ作成およびデータ分析キット | 数学の概念を現実世界の問題に適用する | 統計とデータ解釈 |
| モンテッソーリにおける数学器具 | 金融、統計、エンジニアリングアプリケーション向けの高度なツールのコレクション | 応用数学 |
モンテッソーリ算数教材は、発達段階に合わせて構成されており、子どもたちが基本的な数感覚から高度な問題解決能力まで、論理的に自信を持って学習を進められるようサポートします。これらの教材は、数の関係を理解するための明確で実践的な道筋を示し、子どもたちが単に数学を暗記するだけでなく、数学を心から楽しむことができるようにします。
数学モンテッソーリ教材のこの完全な内訳は、完全なキーワードの網羅、構造化された学習アプローチ、モンテッソーリ数学がどのようにして強力な数学的思考力を養成するかについての実践的な説明を保証します。

完璧な教室はワンクリックで完成します!
モンテッソーリ算数アクティビティと実践学習
モンテッソーリ算数アクティビティは、子どもたちが実践的な探究を通して、数字、パターン、そして数学的な関係性を深く理解できるよう設計されています。暗記と反復に重点を置く従来の算数レッスンとは異なり、モンテッソーリ算数は、体系的なアクティビティを通して能動的な学習を促します。これらのアクティビティでは、モンテッソーリ算数教材を用いて、子どもたちが具体的な経験から抽象的な思考へと移行し、数学の概念を文章で応用する前に、しっかりと理解できるように支援します。
モンテッソーリ算数アクティビティに取り組むことで、子どもたちは力強い問題解決能力、自信、そして数への好奇心を育むことができます。それぞれのアクティビティは、子どもたちが自立した学習をサポートするように綿密に構成されており、子どもたちは自分のペースで数を学びながら、強い数学的思考力を育むことができます。
モンテッソーリ算数アクティビティの設計方法
モンテッソーリ数学アクティビティの構造は、子供たちが数字とその関係を明確かつ論理的に理解できるようにする 4 つの主要原則に基づいています。
実践的な探求を通して学ぶ
子どもたちは数学モンテッソーリ教材を使って数学の概念を体験します 身体的にも視覚的にも事実を暗記する代わりに、数字に触れ、動かし、操作することで、数学的な概念との強い神経的つながりを形成するのに役立ちます。
具体的な思考から抽象的な思考へ
モンテッソーリ算数アクティビティは、具体的なものから始めて、記号や方程式を導入する段階的な学習プロセスに沿って進められます。例えば、お子様はまずゴールデンビーズを使って位取りを学び、その後紙に数字を書きます。
自己修正と自主的な発見を奨励する
モンテッソーリ算数メソッドの核となる側面は、子供たちが自ら間違いを認識し、修正できるようにすることです。 モンテッソーリ数学教材の多くは自己修正型であり、大人の介入なしに子供が間違いを認識し、アプローチを調整できることを意味します。
構造化されながらも柔軟な学習
モンテッソーリ算数カリキュラムは体系的な学習パスを提供しますが、子どもたちは算数の概念を自主的に探求することができます。このアプローチにより、子どもたちはより複雑なトピックに進む前に、それぞれの数学的概念を完全に習得することができます。
これらの原則により、モンテッソーリ数学アクティビティは非常に効果的で、魅力的であり、さまざまな年齢や学習スタイルの子供たちが参加できるようになります。
0~3歳児向けのモンテッソーリ算数アクティビティ
0~3歳の乳幼児を対象としたモンテッソーリ算数アクティビティは、感覚認識、空間認識、そして早期パターン認識の発達に重点を置いています。この段階の子どもたちはまだ正式な数字を学習していませんが、形、大きさ、順序、物体の永続性などを探求することで、将来の数学的思考の基礎を築く活動に取り組みます。
1. 感覚と空間認識の活動
- 物体の永続性ボックスの探索 – 物体は見えなくても存在し続けることを子どもたちに理解させ、早期の論理的思考力を養います。
- ノブ付きシリンダーの分類 – 子どもたちはノブ付きシリンダーをサイズ順に並べることで、高さと幅の段階を認識できるようになります。
- 積み重ねと入れ子のカップ – 子どもたちが、初期の数学認知における基本的なスキルである、大きさの関係と順序を探求することを奨励します。
2. パターンと形状の認識
- 形を分類するボックスゲーム – 子どもたちが円、正方形、三角形を対応するスロットに一致させるのを助けることで、基本的な幾何学を紹介します。
- ペグとリングのスタッキング – 将来の計算に不可欠なスキルである一対一対応を強化しながら、細かい運動能力を強化します。
- 触覚カウントディスク – 触覚と動きを通して、グループ化と数量の区別を早期に導入します。
これらの活動は、感覚の探究、空間認識、早期の問題解決の強固な基盤を提供し、子供たちが後の正式な数学の学習に備えられるようにします。


3~6歳のお子様に最適なモンテッソーリ算数ゲーム
3歳から6歳までのお子様向けのモンテッソーリ算数アクティビティは、数感覚、数え方、そして算数の早期習得に重点を置いています。これらのアクティビティでは、モンテッソーリ算数教材を用いて、遊びながらインタラクティブに算数を学ぶことで、お子様が数字を日常生活の楽しい一部として捉えられるよう促します。
1. 数字の認識と数え方
- ナンバーロッドマッチング – 子どもたちは数字を順番に並べ、数字を識別し、その長さを比較することを学びます。
- サンドペーパー数字トレース – サンドペーパーナンバーを使用すると、子供たちは数字を声に出して読みながらなぞり、触覚、音、動きを通じて数字の認識を強化します。
- スピンドルボックスカウント – 子どもたちは正しい数のスピンドルをコンパートメントに配置することで、数字と実際の量を関連付けるのに役立ちます。
2. 初期の算数ゲーム
- ゴールデンビーズ追加 – 子どもたちはゴールデンビーズを使って数量を組み合わせ、基本的な加算の概念を学びます。
- 追加ストリップボードレース – 加算ストリップボードを使用して、子供たちは簡単な方程式を実践的に解きます。
- 引き算のヘビゲーム – この楽しいアクティビティでは、色付きのビーズを使用して、引き算を視覚的かつインタラクティブな体験に変えます。
3. 実践的な形とパターンの探求
- 幾何学的形状の分類 – 子どもたちは幾何学的なキャビネットを使って、側面、角、パターンに基づいて形を分類します。.
- 建設的な三角形のパズル – 子どもたちは構成三角形を使って大きな形を作り、幾何学と空間関係の理解を深めます。
若い学習者向けのこれらのモンテッソーリ数学アクティビティは、数感覚、算術、パターン認識の強固な基礎を提供し、より高度な数学の概念に十分備えることができます。



6~12歳のお子様に最適なモンテッソーリ算数アクティビティ
6歳から12歳までのお子様向けのモンテッソーリ算数アクティビティは、基本的な数の知識を深め、複雑な計算、分数、そして問題解決能力を養います。これらのアクティビティは、体系的な探究を通して、位取り、掛け算、割り算、そして幾何学への理解を深めるのに役立ちます。
1. 位取りと大きな数の探究
- ゴールデンビーズ位取りゲーム – 子どもたちはゴールデンビーズを使って千、百、十、一を表し、十進法の理解を深めます。
- スタンプゲーム算数 – このゲームは、子供たちがゴールデンビーズから数字の書き方に移行し、抽象的な計算の準備をするのに役立ちます。
- ドットゲームチャレンジ – 位取りの理解を深めながら、足し算と引き算を楽しく練習できます。
2. 多桁の計算と分数
- チェッカーボードの掛け算 – チェッカーボードを使用すると、子供たちは大きな数字を視覚的に掛け算し、数字のパターンを理解できるようになります。
- 試験管部門レース – このゲームは、長割り算を実践的なアクティビティに変え、理解しやすくします。
- 分数インセットマッチング – 子どもたちは分数インセットを使用して、さまざまな分数のサイズを比較し、分数の等価性について学びます。
3. 幾何学と高度な数学の概念
- ピタゴラスの定理ボード – このアクティビティでは、直角三角形と正方形を使用してピタゴラスの定理を紹介します。
- 代数ペグボードチャレンジ – 子どもたちはペグを使ってパターンや方程式を解くことで、初等代数を学習します。
- 建設的三角形の調査 – 複雑な幾何学的概念を探求する実践的な方法。
これらのアクティビティは、数学を学ぶための構造化されたインタラクティブなアプローチを提供し、子供たちが数学的推論に自信と流暢さを身に付けることを保証します。
モンテッソーリ算数アクティビティは、あらゆる年齢の子どもたちが算数を楽しく、インタラクティブで、有意義に学べるよう設計されています。モンテッソーリ算数教材を使用することで、子どもたちは体験を通して学び、算数の概念に対する深く永続的な理解を育むことができます。
実践的な学習、構造化されたアクティビティ、独立した発見の組み合わせにより、モンテッソーリ数学は、数学を自然に楽しく教えるための最も効果的な方法の 1 つとなっています。



家庭でモンテッソーリ算数を実践する
モンテッソーリ算数を家庭環境に取り入れることで、子どもたちは学校以外でも自然と実践的な学習を続けることができます。多くの親御さんは、モンテッソーリ算数教材は教室でのみ使うものだと考えていますが、適切なアプローチをとれば、モンテッソーリ算数は家庭でも効果的に実践できます。構造化されながらも柔軟な学習環境を作り、DIYモンテッソーリ算数教材を活用し、自発的な探究心を育むことで、親御さんは快適で馴染みのある環境で子どもたちの数学的な思考力を育むことができます。
親が自宅でモンテッソーリ算数を教える方法
モンテッソーリ算数を家庭で教えるのに、教室のような設備は必要ありませんが、考え方を変える必要があります。暗記やワークシートに重点を置くのではなく、保護者は以下の点に留意すべきです。
- 実践的な学習を活用する – 子どもたちがモンテッソーリ数学教材に触れ、実際の経験を通して数学の概念を発見できるように促します。
- 段階的なアプローチに従う – 具体的な学習から抽象的な学習へと移行しながら、数学のアクティビティを構造化された順序で提示します。
- 自主的な探求を奨励する – 自己指導型モンテッソーリ数学アクティビティを使用して、子供たちが間違いを犯し、自分で修正できるようにします。
- 数学を日常生活の一部に – 料理の材料を測ったり、家の中にある物を数えたりするなど、モンテッソーリ数学の概念を日常生活に応用します。
親がモンテッソーリ数学を自然な経験に取り入れると、子どもは数学を単なる学校の科目ではなく、実用的で有意義なものとして見るようになります。
モンテッソーリ算数教材とアクティビティを自分で作る
親は簡単な家庭用品を使って DIY の数学モンテッソーリ教材を作成し、高価な教室用具を使わずにモンテッソーリ数学アクティビティに参加することができます。
1. 数感覚と数え方を学ぶアクティビティ
- DIYナンバーロッド – 増加する数値を表すために色付きの紙片やブロックを使用し、子供が数量と数の順序を視覚化できるようにします。
- 手作りサンドペーパー番号 – サンドペーパーから数字を切り取り、厚紙に貼り付けて、子どもたちが数字の形をなぞったり感じたりできるようにします。
- 家庭用品を使ったスピンドルカウント – スピンドル ボックスをアイスキャンディーの棒、ストロー、洗濯ばさみなどに置き換えて、1 対 1 の対応と数字の認識を強化します。
2. 算数と位取りのアクティビティ
- ビーズとカップを使ったゴールデンビーズの位取り – 小さなビーズを使って単位、十、百、千を作り、モンテッソーリ数学の位取りの概念を強化します。
- DIY足し算・引き算ボード – 段ボールに足し算のストリップボードを描き、色付きの紙のストリップを使用して基本的な演算を示します。
- 手作りの掛け算ボード – 小さな穴の開いた厚紙にビーズやボタンを押し込み、視覚的なパターンを通して掛け算を練習します。
3. 幾何学と測定の活動
- DIY幾何学模様のキャビネット – 基本的な幾何学的形状を厚紙から切り取り、子供たちに輪郭に合わせてもらいます。
- 建設的な三角形のパズル – さまざまな色とサイズの三角形を切り取り、子供たちがより大きな形を形成できるようにします。
- 日常の物を使った測定 – 定規、メジャー、またはおもちゃのブロックなどの非標準の単位を使用して、長さと比較を教えます。
DIY 数学モンテッソーリ教材を遊びに取り入れることで、子供たちはモンテッソーリ数学アクティビティに自然と参加し、数学がインタラクティブで楽しいものになります。
モンテッソーリ算数学習のための家庭環境づくり
モンテッソーリ算数を家庭で実践するには、環境を整えることが鍵となります。目標は、自立した学習をサポートし、自己修正を促し、モンテッソーリ算数教材にアクセスできる空間を作ることです。
1. モンテッソーリ算数教材の整理
- 数学モンテッソーリ教材を、アクセスしやすい低い棚に並べ、子供たちが自分の活動を選べるようにします。
- 教材はシンプルかつ整理された状態に保ち、子供たちが一度に 1 つの概念に集中できるようにします。
- お子様の進歩に応じて教材をローテーションし、以前の概念を習得したら新しいアクティビティを導入します。
2. 自立した作業を奨励する
- プレッシャーや時間制限を避け、子供たちが自分のペースでモンテッソーリ数学を学べるようにします。
- 小さなテーブルやフロアマットなど、子供が集中できる透明な作業スペースを用意します。
- 介入するのではなく観察する - モンテッソーリ数学は自己修正と個人的な発見を重視します。
家庭環境が自立した学習をサポートするように整えられると、子どもは数字に対する深い理解を育み、数学的能力に自信を持つようになります。

モンテッソーリ数学と現代教育の未来
教育の進化に伴い、モンテッソーリ算数はSTEM教育、デジタルツール、そして現代的な教育法と融合しながら適応していきます。モンテッソーリ算数の未来は、伝統的な実践的な教材と革新的なテクノロジーを組み合わせ、子どもたちが基礎的かつ高度な数学スキルを身につけられるようにすることにあります。
モンテッソーリ数学とSTEM教育の統合
モンテッソーリ数学を STEM 教育に取り入れることで、子どもたちは数学の概念を科学、工学、テクノロジーと結び付けることができます。 子どもたちは、数学モンテッソーリ教材とSTEMベースの活動を組み合わせることで、現実世界の問題解決能力を養います。.
1. 数学モンテッソーリ教材とSTEMの連携
- ゴールデンビーズとエンジニアリングコンセプト – 探検 位取り 物理的な材料を使って構造物を構築するとき。
- 幾何学的なキャビネットとコーディングの基礎 – 形状と空間的推論を理解することは、コンピュータープログラミングに不可欠です。
- 測定と科学実験 – 定規、計量カップ、スケールを使用して物理学と化学の実験を探究します。
モンテッソーリ数学と STEM 教育を統合することで、子どもたちは数字についての実践的な理解を身につけ、テクノロジーと科学の分野での将来のキャリアに備えることができます。
デジタルツールとモンテッソーリ算数:現代的なアプローチ
モンテッソーリ算数は伝統的に実践的な教材に依存してきましたが、現代のテクノロジーはインタラクティブなデジタルツールを提供することで学習効果を高めることができます。多くの学校や保護者が、物理的な教材を補完するために、デジタル版モンテッソーリ算数アクティビティを活用しています。
1. デジタルモンテッソーリ算数ツールの利点
- 仮想マニピュレータ – ゴールデンビーズ、ナンバーロッド、分数インセットのオンラインシミュレーションは、学習の強化に役立ちます。
- モンテッソーリ算数アプリ – インタラクティブなゲームにより、子供たちは自分のペースで魅力的な方法で数え方、算数、幾何学を練習できます。
- オンラインモンテッソーリ学習プラットフォーム – デジタル プログラムは、モンテッソーリ数学カリキュラムに沿った構造化されたレッスンを提供します。
デジタルツールを従来のモンテッソーリ数学教材と統合することで、子どもたちは物理的な学習体験と仮想的な学習体験を組み合わせたバランスの取れた学習アプローチを体験します。
モンテッソーリ算数の未来は、その中核となる原則を維持しながら進化していく力にあります。モンテッソーリ算数教材を現代のテクノロジー、STEM教育、そして家庭学習環境と融合させることで、子どもたちは絶えず変化する世界で成功するための確かな数学的思考力を育み続けることができるでしょう。
結論
モンテッソーリ算数は、算数への包括的かつ実践的なアプローチを提供し、子どもたちが数字、パターン、そして問題解決能力を理解するのを助けます。モンテッソーリ算数教材を用いることで、子どもたちは具体的な探求から抽象的な推論へと段階的に進み、単なる公式の暗記ではなく、数学の概念を完全に理解できるようになります。
モンテッソーリ算数カリキュラムは、幼児期から思春期にかけての子どもたちの自立した学習をサポートし、解決策の発見、自己修正、論理的思考の発達を促します。このメソッドは、学校でも家庭でも、魅力的で効果的、そして楽しい学習体験を生み出します。
モンテッソーリ算数をSTEM学習、デジタルツール、そして実社会での応用と統合することで、教育の進化に伴い、その効果はさらに高まります。モンテッソーリ算数教材へのアクセスを拡大し、モンテッソーリ算数アクティビティを推進することで、より多くの子どもたちがしっかりとした数学の基礎を身につけ、将来の学業や職業での成功に備えることができます。
モンテッソーリ教育のアプローチを数学に取り入れることで、私たちは子供たちが数学を挑戦としてではなく、発見と学習の刺激的な旅として捉えられるようにします。



